عرض عام
تقريبًا في نفس الوقت التي أتم خلالها إسحاق بن حنين (٨٣٠ م - ٩١٠ م) ** هذه التواريخ تقريبية وثابت بن قرة (٨٣٠ م - ٩٠١ م) ** هذه التواريخ تقريبية أولى الترجمات الجديرة بالاعتماد لكتاب مانالاوس في الأشكال الكرية، كتب ثابت نفسه بحثًا منفصلًا عن النظرية الأساسية في علم حساب المثلثات الكروية اليوناني، وهو <كتاب الشكل القطاع> الذي يعتمد على محدب رباعي الأضلاع مُكوّن من أقواس دوائر كبيرة. بعد ذلك بفترة قصيرة، أنتج أبو الوفاء البوزجاني (٩٤٠ م - ٩٩٨ م) وأبو نصر منصور بن عراق (٩٥٠ م - ١٠٣٦ م) ** هذه التواريخ تقريبية نظريات جديدة على أساس الدوال المثلثية: قوانين الجيب وجيب التمام وخط المماس، وهي دوال مبنية على مصادر هندية. وأخيرًا، في القرنين العاشر والثالث عشر، كتب العالمان الموسوعيان أبو الريحان البيروني (٩٧٣ م - ١٠٤٨ م) ونصير الدين الطوسي (١٢٠١ م - ١٢٧٤ م) بحثين كان من شأنهما أن يضعا أساسًا قويًا لعلم حساب المثلثات الكروية كفرع مستقل من الرياضيات. وهما بحث في أساسيات علم أوصاف الكون (الكوزموغرافيا) <كتاب مقاليد علم الهيئة>، وبحث عن القطاع الدائري <كتاب الشكل القطّاع>، يُعرف أيضًا باسم "رسالة القطّاع في علم الهندسة".
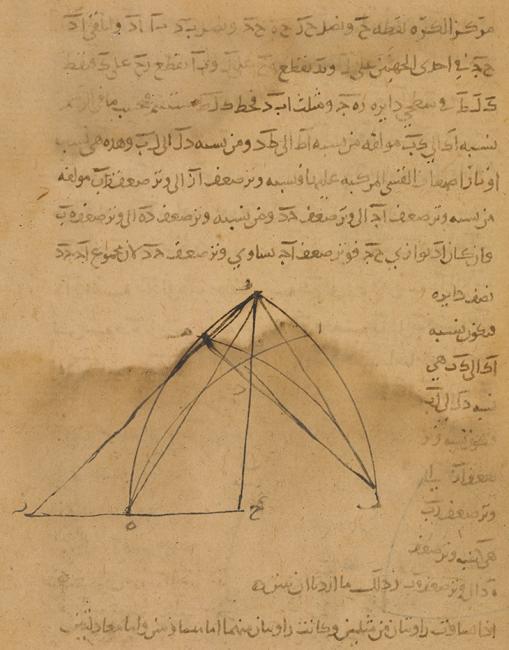
على الرغم من ذلك، لم يكن تفوّق المناهج الجديدة مُسلّم به بالنسبة لكل علماء الرياضيات البارعون. ففي القرن العاشر انتقد أبو سهل الكوهي معاصريه لاعتقادهم بإمكانية حل بعض المسائل الكروية بسهولة أكبر باستخدام النظريات البديلة لنظرية "الشكل القطّاع" – أي بالنظرية التي تستغنى عنها وهي"الشكل المُغني" وأيضاً بنظرية "الشكل الظلّي" – وهما يماثلان رياضيًا قانون جيب الزاوية الكروي وظل الزاوية. بل أن الكوهي أظهر ببراعة إمكانية حل تلك المسائل بكفاءة باستخدام تطبيقات متتالية لنظرية الشكل القطّاع. ونرى هنا التفاعل بين أنماط الرياضيات المختلفة - المناهج الكلاسيكية من ناحية، وابتكارات العصور الوسطى من ناحية أخرى.
إعادة قراءة كتاب <الأشكال الكرية>
درس العلماء الذين عملوا على تطوير علم حساب المثلثات الكروية الجديد كتاب <الأشكال الكرية> العتيق من منظور نقديّ وأنتجوا منه نسخًا جديدة. أنتج أبو نصر منصور بن عراق (٩٥٠ م - ١٠٣٦ م) ** هذه التواريخ تقريبية بإنتاج نسخة جديدة من إحدى الترجمات العربية للنص مضيفًا بعض التعليقات الرياضية والفلكية، كما قام بتغيير واحدًا من الأشكال الأساسية في علم حساب المثلثات الكروية من وتر الدائرة الكلاسيكي إلى جيب الزاوية الأكثر معاصرة. وقام نصر الدين الطوسي (١٢٠١ م - ١٢٧٤ م) فيما بعد باستخدام عدة نسخ من مخطوطات مختلفة في إنتاج مراجعته الشهيرة للنص المعتمد والتي تُعدّ مثالًا رائعًا على الدراسة النقدية، فقد أخذت تلك المراجعة في الاعتبار التاريخ المعقد للنص وتضمنت شروحًا رياضية وفلكية مفصلة. بهذه الطريقة بيّن الطوسي على احترامه سلفًا مهمًا قد بنى على عمله وتفوق عليه في كتابه <كتاب الشكل القطّاع> – وهو معالجة رياضية كامل لعلم حساب المثلثات المستوية والكروية كفرع من فروع الرياضيات البحتة، باستخدام الطريقة القديمة لنظرية "الشكل القطّاع" جنبًا إلى جنب مع النظريات الجديدة الأكثر ثراءً التي أخرجها العلماء في العصر الإسلامي.

كتاب <الأشكال الكرية> باللغة اللاتينية
قبل قرن من كتابة الطوسي لدراسته، أصدر جيراردو الكريموني (١١١٤ م - ١١٨٧ م) ** هذه التواريخ تقريبية في توليدو بأسبانيا، ترجمة لاتينية لكتاب <الأشكال الكرية> لمانالاوس من نسخة عربية أخرى كانت بالمحتمل مزيجًا من ترجمتين معروفتين، وقد فُقِدت هذه النسخة الآن. وبعد ذلك بقرون عديدة، في أوائل القرن الثامن عشر، أصدر إدموند هالي (١٦٥٦ م - ١٧٤٢ م)، الأستاذ الجامعي السافيلي (وهو منصب مرموق في جامعة أكسفورد العريقة) والذي شغل منصب الفلكي الملكي، إصدارًا لاتينيًا جديد، مأخوذ هذه المرة من الترجمة العبرية لجاكوب بن ماهر (١٢٣٦-١٣٠٤). وقد اعتمدت الأخيرة على نفس المصدر العربي الذي أُخذت عنه نسخة جيرارد اللاتينية، مع بعض الإضافات من نسخة مختلفة عربية أقدم. كما استخدم هالي أيضًا نسخة لاتينية متخصصة بالرياضيات تعود إلى فرانشيسكو موروليكو (١٤٩٤-١٥٧٥). قام هالي، مثلما قام موروليكو من قبله، بتغيير النص بطرق مختلفة للوصول إلى ما اعتقد أنه الأقرب رياضيًا مما قصده مانالاوس.

تتضح كذلك في التراث اللاتيني حقيقة أن كتاب <الأشكال الكرية> كان موروثًا على الأغلب دون قدر كبير من الفهم. في مخطوطة أخرى في المكتبة البريطانية، Harley MS 13، نكتشف مقتطفًا من ترجمة جيرارد. إلا أن هذا البحث لا يتضمن أية رسوم بيانية وينتهي فجأة بعد تقديم عدة افتراضات دون إتمام المسألة، مما يجعله عديم الفائدة رياضياَ. وفي هذه الحالة، فإن نقل الرسالة قد تم بأغراض تكاد تكون تزيينية، للاحتفاء بالقيمة التاريخية والثقافية دون فائدة عملية.
جسر بين القديم والجديد
لم يعتبر علماء الرياضيات في العصور القديمة والعصور الوسطى الأفكار الجديدة في أعمالهم بمثابة تجاوز تام لأساطين الماضي. فبينما قاموا بتطوير نظريات ومناهج رياضية جديدة، استمروا أيضًا في دراسة وتنقيح ومناقشة الأعمال القديمة - ليس كمجرد تحف تاريخية ولكن كمصادر قيّمة للعلوم الرياضية وكمصادر إلهام لتطوير تلك العلوم من طرفهم.


